von Norbert Giesinger (aus Zeitensprünge 2/2011)
Joseph Ashbrook erwähnt im August 1972 in Sky and Telescope einen Bericht des Simeon (Symeon) von Durham (um 1060–1130) und seine Zuordnung auf das rückgerechnete Ereignis von 755 AD – Mondfinsternis mit gleichzeitiger oder unmittelbar anschließender Jupiterbedeckung.
Der belgische Meteorologe und Astronom Jean Meeus hat, neben der Erstellung des Fundamentalwerkes Kanon der Sonnenfinsternisse / Kanon der Mondfinsternisse, zusammen mit Hermann Mucke, die weitbekannten Astronomical Algorithms und einige Bücher zu Finsternissen und Bedeckungen geschrieben.
Im seinem Buch Mathematical Astronomy Morsels von 1997 gibt Meeus auch eine Darstellung von Planetenbedeckungen bei Mondfinsternissen, mit deren Berechnung er sich mit Co-Autoren schon 1977 beschäftigt hat [Meeus/Maanen/Können]. Aus zahlreichen Arbeiten, Veröffentlichungen und Korrespondenzen ist Seriosität und tiefgreifende Kenntnis von Meeus zu derartigen Fragen zu ersehen.
Von Kap. 23 “Occultations of planets by the eclipsed moon” des Buches sind vor allem die Jupiterbedeckungen von historischem Interesse, insbesondere wegen einer Überlieferung des Simeon von Durham aus dem 12. Jh. Dessen Überlieferung einer Jupiterbedeckung bei einer Mondfinsternis im Jahr 754 wurde einem rückgerechneten Ereignis 755 AD zugeschrieben. Das Ereignis wurde in Veröffentlichungen und Internetforen der letzten 15 Jahre als sehr selten oder gar einzigartig betrachtet und als starker Hinweis oder fast als Beweis gegen die Phantomzeithypothese von Heribert Illig angesehen.
Was zeigen die Berechnungen und Ergebnisse bzw. Tabellen von Meeus? Sie zeigen, dass derartige Jupiterbedeckungen zwar selten sind, aber seit der Antike öfters stattfanden. (Nach 1531 ist allerdings erst wieder 2932 eine Mondfinsternis mit Jupiterbedeckung zu erwarten.)
Die Daten in den Tabellen von Meeus sind Ergebnisse rigoroser himmelsmechanischer Kalkulation. Nachgerechnet (mit Anwendung der in seinen Astronomical Algorithms angegebenen Methodik) habe ich sie nicht, da müsste ich mich weiter einarbeiten; ich vertraue aber der Expertise von Jean Meeus. Eine genauere Betrachtung der Tabelle zeigt das mehrfache Auftreten gleicher Zeitabstände zwischen den Ereignissen.
Bei Einschluss der Sichtbarkeitsbedingungen, d.h. z.B. mit der Forderung der jeweiligen Beobachtbarkeit des Ereignisses in Europa und einer wesentlichen (nicht notwendigerweise totalen) Größe der Finsternis reduziert sich die Tabelle auf wenige Ereignisse.
Ergebnisse von Meeus
Tabelle 1, von Meeus modifiziert, nur Jupiterbedeckungen berücksichtigt
| Datum (Jul./ Greg.) A.D. – Zählung |
Maximum der Finsternis (TD) |
Größe der Mondfinsternis |
Sichtbarkeit (SH, Äqu, NH) * |
Julianische Tageszahl JD |
| 01. Dezember 103 | 15:14 | 0.21 | Äqu | 1759012.6 |
| 29. Juni 158 | 12:00 | 0.63 | NH | 1778947.0 |
| 17. Dezember 400 | 20:29 | 1.06 | Äqu | 1867509.4 |
| 07. November 458 | 00:18 | 0.80 | NH | 1888652.5 |
| 03. Mai 524 | 19:37 | 1.65 | SH | 1912572.3 |
| 23. November 755 | 19:33 | 1.40 | NH | 1997148.3 |
| 21. Juli 799 | 16:23 | 1.55 | NH | 2013094.2 |
| 20. Juni 810 | 20:34 | 1.84 | Äqu | 2017063.4 |
| 20. Mai 821 | 21:04 | 1.41 | Äqu | 2021068.4 |
| 10. April 879 | 11:46 | 1.36 | SH | 2042212.0 |
| 19. Januar 995 | 15:53 | 1.25 | Äqu | 2084500.2 |
| 08. Dezember 1052 | 22:42 | 1.65 | NH | 2105643.4 |
| 25. April 1176 | 19:26 | 0.67 | SH | 2150707.3 |
| 17. März 1234 | 03:38 | 0.65 | SH | 2171851.7 |
| 15. November 1407 | 12:49 | 1.19 | NH | 2235283.0 |
| 14. Oktober 1418 | 22:09 | 1.12 | NH | 2239269.4 |
| 12. Juni 1462 | 01:58 | 0.59 | SH | 2255215.6 |
| 12. Mai 1473 | 07:28 | 0.37 | Äqu | 2259202.8 |
| 01. April 1531 | 18:47 | 0.11 | SH | 2280346.3 |
| 10. Juni 2932 | 00:01 | 0.20 | Äqu | 2792111.5 |
| 01. Mai 2990 | 01:40 | 0.09 | SH | 2813255.6 |
TD: Angabe in Dynamischer Zeit. Für UT (Universalzeit) um Delta T zu korrigieren.
* Äqu = Äquator, NH = Nördliche Halbkugel, SH = Südliche Halbkugel
Tabelle 2
Nur auf der Nordhalbkugel in Europa (Nacht/Dämmerung) freisichtig beobachtbare Ereignisse. Die Tabelle reduziert sich für Europa ganz wesentlich auf die Ereignisse:
| Datum (Jul./ Greg.) A.D. – Zählung |
Maximum der Finsternis (TD) |
Größe der Mondfinsternis |
Sichtbarkeit (SH, Äqu, NH) |
Julianische Tageszahl JD |
| 07. November 458 | 00:18 | 0.80 | NH | 1888652.5 Fr |
| 23. November 755 | 19:33 | 1.40 | NH | 1997148.3 So |
| 08. Dezember 1052 | 22:42 | 1.65 | NH | 2105643.4 Di |
| 14. Oktober 1418 | 22:09 | 1.12 | NH | 2239269.4 Fr |
TD: Angabe in Dynamischer Zeit. Für UT (Universalzeit ) um Delta T zu korrigieren.
Dem berechneten Ereignis vom 23. November 755 AD wird die Überlieferung einer Beobachtung durch Simeon von Durham zugeschrieben. Die Berechnungen sind rein himmelsmechanisch (Angaben in TD) und beinhalten als Anbindung an schriftliche Überlieferungen nur den Kalenderübergang von 1582. Da uns aber nur frühere Ereignisse interessieren, kommt nur der Julianische Kalender zum Tragen. Meeus schreibt [1997, 151]:
„The Jupiter case of A.D. 755 is of particular interest, since this occultation has been observed and recorded by Simeon of Durham in England (*). I have found that, for Durham, the immersion of Jupiter took place about 20 minutes after the end of totality (+), while the emersion occurred shortly after the last contact of the Moon with the umbra. Using the value of +35 minutes for the difference Delta T between Dynamical Time and Universal time, the following results are obtained:
Maximum eclipse 18 h 43 m UT
End of totality 19 h 28
Immersion of Jupiter 19 h 48
End of partial phase: 20 h 37
Emersion of Jupiter 20 h 39Even for a value of Delta T as small as +35 minutes, the results are similar. Jupiter was occulted by the northern part of the eclipsed moon. The remarkable fact appearing from Table 23.A is the irregular distribution of the events involving Jupiter. While there were four cases during the 15th century, there is none between the years 1531 and 2932. The explanation for this is not easy, and can be found in the original article.“
[Mit (*) zitiert Meeus Ashbrook [1972, 85] und Newton [1972].
Die Bemerkung von Meeus “Using the value of + 35 minutes […] Even for a value of Delta T as small as +35 minutes, the results are similar” ist bemerkenswert. Meeus verwendet einen Wert Delta T von 50 Minuten, der zum Jahr 850 passt und weiters sogar nur von 35 Minuten, dem Wert für das Jahr 1000 und nicht für 755. Meeus verwendet also deutlich bis wesentlich kleinere Werte für Delta T, als sich aus der Tabelle im Buch [1997, ab 10] ergeben würden. Meeus schreibt im Buch, dass die Verteilung der Ereignisse irregulär ist, in der Arbeit von 1977 steht das aber nicht.
Die Abstände aufeinanderfolgender Ereignisse sind:
| Datum (Jul./Greg.) | Jul. Tageszahl | Abstand in Tagen (d) |
Abstand in a, m, d |
| 01. Dezember 103 | 1759012.6 | ||
| 29. Juni 158 | 1778947.0 | 19934.4 | 54a 6 m 29 d |
| 17. Dezember 400 | 1867509.4 | 88562.4 | 242a 5 m 22 d |
| 07. November 458 | 1888652.5 | 21144 | 57a 10 m 22 d |
| 03. Mai 524 | 1912572.3 | 23919 | 65a 5 m 27 d |
| 23. November 755 | 1997148.3 | 84576 | 231a 6 m 24 d |
| 21. Juli 799 | 2013094.2 | 15946 | 43a 7 m 28 d |
| 20. Juni 810 | 2017063.4 | 3987 | 10a 11 m 1 d |
| 20. Mai 821 | 2021068.4 | 3987 | 10a 11 m 1 d |
| 10. April 879 | 2042212.0 | 21144 | 57a 10 m 22 d |
| 19. Januar 995 | 2084500.2 | 42288 | 115a 9 m 13 d |
| 08. Dezember 1052 | 2105643.4 | 21143 | 57a 10 m 21 d |
| 25. April 1176 | 2150707.3 | 45064 | 123a 4 m 19 d |
| 17. März 1234 | 2171851.7 | 21145 | 57a 10 m 23 d |
| 15. November 1407 | 2235283.0 | 63431 | 173a 8 m 2 d |
| 14. Oktober 1418 | 2239269.4 | 3986 | 10a 10 m 30 d |
| 12. Juni 1462 | 2255215.6 | 15947 | 43a 7 m 29 d |
| 12. Mai 1473 | 2259202.8 | 3987 | 10a 11 m 1 d |
| 01. April 1531 | 2280346.3 | 21143 | 57a 10 m 21 d |
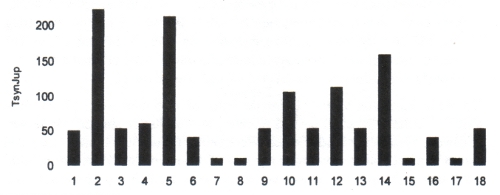
Die Verteilung der zeitlichen Abstände aller Ereignisse untereinander zeigt, dass genau gleiche zeitliche Abstände mehrfach auftreten. In nachstehender Abb. 1 sind die zeitlichen Zeitabstände der jeweils aufeinander folgenden Ereignisse dargestellt (von 1-2 bis 18-19) in Einheiten von TsynJup (mittlere synodische Periode des Jupiter). Sie beträgt 398.88 mittlere Sonnentage. Der Wert schwankt zwischen 396 und 403 Tagen. Grund sind vor allem die Exzentritäten von Jupiter- und Erdbahn. Die zeitlichen Abstände sind für die mittlere TsynJup von 398,88 Tagen fast genau ganzzahlig, bei Berücksichtigung der Schwankung immer ganzzahlig. Bemerkenswert ist der Abstand von 2144 Tagen (53 TsynJup), dieser tritt 5-mal, mit Verdoppelung und Vervierfachung 7-mal auf.
Nur für Nordhalbkugel (alle Tageszeiten) gilt:
| Datum (Jul./ Greg.) A.D. – Zählung |
Julianische Tageszahl JD |
Abstand in Tagen |
Abstand (Jahre, Monate, Tage) |
TSynJup |
| 01. Dezember 103 | 1759012.6 | |||
| 29. Juni 158 | 1778947.0 | 19934 | 54 6 29 | 50 |
| 07. November 458 | 1888652.5 | 109706 | 300 4 13 | 275 |
| 23. November 755 | 1997148.3 | 108495 | 297 0 16 | 272 |
| 08. Dezember 1052 | 2105643.4 | 108495 | 297 0 16 | 272 |
| 15. November 1407 | 2235283.0 | 129640 | 354 11 11 | 325 |
| 14. Oktober 1418 | 2239269.4 | 3986 | 10 10 30 | 10 |
Nur für Nordhalbkugel/Europa sichtbare/beobachtbare Ereignisse:
| Datum (Jul./ Greg.) A.D. – Zählung |
Julianische Tageszahl JD |
Abstand in Tagen |
Abstand (Jahre, Monate, Tage) |
TSynJup |
| 07. November 458 | 1888652.5 | |||
| 23. November 755 | 1997148.3 | 108495 | 297 0 16 | 272 |
| 08. Dezember 1052 | 2105643.4 | 108495 | 297 0 16 | 272 |
| 14. Oktober 1418 | 2239269.4 | 133626 | 365 10 9 |
Für die in Europa sichtbaren Ereignisse tritt der Abstand 297a 2-mal hintereinander auf:
| Datum (Jul./Greg.) A.D. – Zählung |
Maximum der Finsternis (TD) |
Größe der Mondfinsternis |
Jul. Tageszahl JD |
| 07. November 458 | 00:18 | 0.80 | 1888652.5 |
| 23. November 755 | 19:33 | 1.40 | 1997148.3 |
| 08. Dezember 1052 | 22:42 | 1.65 | 2105643.4 |
| 14. Oktober 1418 | 22:09 | 1.12 | 2239269.4 |
Abstände der Ereignisse, beobachtbar auf der Südhalbkugel bzw. am Äquator:
| Datum (Jul./ Greg.) A.D. – Zählung |
Julianische Tageszahl JD |
Abstand in Tagen |
Abstand (Jahre, Monate, Tage) |
TSynJup |
| 10. April 879 | 2042212.0 | |||
| 25. April 1176 | 2150707.3 | 108495 | 297 0 16 | 272 |
| 17. März 1234 | 2171851.7 | 21145 | 57 10 23 | 53 |
| 01. April 1531 | 2280346.3 | 108494 | 297 0 15 | 272 |
Südhalbkugel:
| Datum (Jul./Greg.) A.D. – Zählung |
Maximum der Finsternis (TD) |
Größe der Mondfinsternis |
Jul. Tageszahl JD |
| 10. April 879 | 11:46 | 1.36 | 2042212.0 |
| 25. April 1176 | 19:26 | 0.67 | 2150707.3 |
| 17. März 1234 | 03:38 | 0.65 | 2171851.7 |
| 01. April 1531 | 18:47 | 0.11 | 2280346.3 |
Diese Jupiterbedeckungen (zudem nur die erste bei totaler Mondfinsternis) sind weniger interessant, da keinerlei Beobachtungen dazu vorliegen.
Der Abstand T297 (108495 Tage d.h. 297 Jahre und 15 bzw. 16 Tage) tritt insgesamt 6-mal auf.
Von Bedeutung sind die in Europa beobachtbaren Ereignisse:
| Datum (Julianisch) | Julianische Tageszahl JD |
Abstand | Größe d. Finsternis |
Anmerkungen |
| 07. Nov. 458 | 1888652.5 | 0.80 | Siehe Anmerkung unten |
|
| 23. Nov. 755 | 1997148.3 | 297a 0m 16d | 1.40 | Der Überlieferung des Simeon v. Durham zugeordnet |
| 08. Dez. 1052 | 2105643.4 | 297a 0m 16d | 1.65 | Jahrzehnte vor den Arbeiten des S. v. Durham. Berichte von Beobachtern zu Lebzeiten Simeons an ihn möglich |
| 14. Okt. 1418 | 2239269.4 | 365a 10m 9d | 1.12 | Keine Berichte bekannt, Lebenszeit des Johannes v. Gmunden |
Wie die Berechnungen von Meeus zeigen, verliert sich der Wert 297 a ab 1531.
Der Abstand von 297 Sonnenjahren zwischen 755 und 458 in der Tabelle von Meeus ist schon Krojer aufgefallen [2003, 201], allerdings erwähnt er nur diese beiden rückgerechneten Ereignisse. Die rückgerechnete Finsternis von 458 ist mit 0,80 eine tief partielle Finsternis. Krojer [201] schreibt:
„allerdings handelte es sich um eine partielle Mondfinsternis, während die Überlieferung Simeons viel mehr auf eine totale Mondfinsternis hindeutet.“
Ich kann das aus den Texten der Übersetzungen der Überlieferung bei Krojer [196-198] nicht ersehen.
Das Jahr 458 fällt in die Chronik des Hydatius (Bischof in Chiaves/Portugal, 379–ca. 468). Ab 428 soll Hydatius eigene Erfahrungen in die Chronik eingebracht haben. Vielleicht ist etwas in seiner Chronik zu finden. Berichte der Chronik werden den Sonnenfinsternissen 418 und 447 zugeordnet.
Abgesehen von zu erwartenden Verformungen [siehe z.B. Demandt 1970] (Simeon von Durham hat eher nicht selbst beobachtet, er war Überlieferer, Kompilator) muss ich bemerken, dass ein Anblick Jupiters, fast berührend neben einem mit 0,8 verfinsterten Mond, ein spektakulärer Anblick ist. Ich behaupte das nach meinen Beobachtungen vieler Mondfinsternisse in den letzten 50 Jahren und nach Beobachtungen von Venusbedeckungen durch den Mond (ohne Verfinsterung!) am Tag und am Abend. Wenn wirklich etwas auf eine totale Finsternis hindeutet, dann muss man die Finsternis von 1052 mit ihrer extremen Dauer und Tiefe diskutieren! Ich zitiere weiter den Text bei Krojer [196]:
„Der lateinische Text der »Symeonis monachi opera omnia«, der mit der Handschrift sprachlich übereinstimmen dürfte, lautet […]
Luna autem xv. sanguineo rubore superducta viii. kal. Decembris xv. aetate, id est, plena luna“.
Dazu wird Durham von F. Richard Stephenson zitiert, der ausgehend von der lateinischen Fassung übersetzt:
“AD 756 […] Also the moon was covered with the redness of blood on the 8th day before the Kalends of December (Nov 24), in the 15th day of its age, that is full moon. And the darkness gradually decreasing, it returned to its original light. Further, astonishingly, a bright star following that same moon, and passing through it, preceded the luminary by as great a space as it had followed it before it was obscured.”
Krojer schreibt (s.o.): „der mit der Handschrift sprachlich übereinstimmen dürfte“. Man kann das „dürfte“ angesichts häufiger Verformungen aber nicht als selbstverständlich annehmen. Noch einmal Meeus: „The Jupiter case of A.D. 755 is of particular interest, since this occultation has been observed and recorded by Simeon of Durham in England”. Dem ist nach der bekannten bzw. vermuteten Überlieferungskette nicht so. Der Simeon zugeordnete Text in der Historia Regum überlebte in einem einzigen Manuskript, der Corpus Christi College Cambridge, MS139, das Ende des 12. Jh. niedergeschrieben wurde, d.h. 1 bis 2 Generationen nach Simeons Tod. Dessen Autorenschaft wird aber auch lt. Wikipedia von modernen Historikern angezweifelt [MS 139].
Die Überlieferungskette ist verknäuelt und heute kaum mehr zu entwirren. Der Bericht stammt aus Aufzeichnungen, die Simeon kompiliert hat, der Bericht in der Historia regum in der MS139 wurde gar nicht von Simeon kompiliert, vielleicht hat Simeon oder sonst jemand doch eine eher zeitgenössische Erscheinung, nämlich die Finsternis von 1052, überliefert.
Auch bei Texten aus dem späten 11. Jahrhundert scheint zu gelten: Wenn man an der Oberflächenschicht kratzt (an der „duricrust“), kommt Treibsand zum Vorschein.
Anblick der Ereignisse
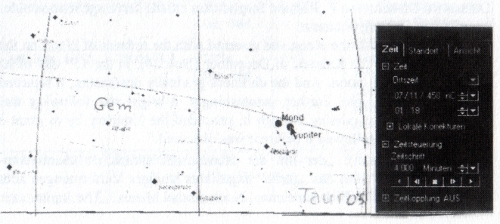
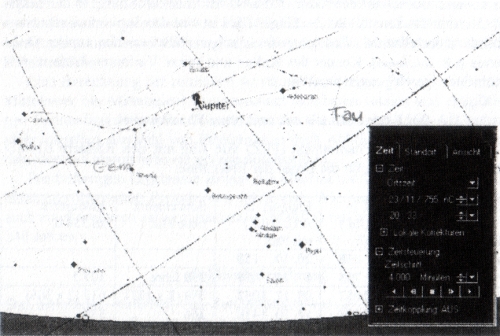
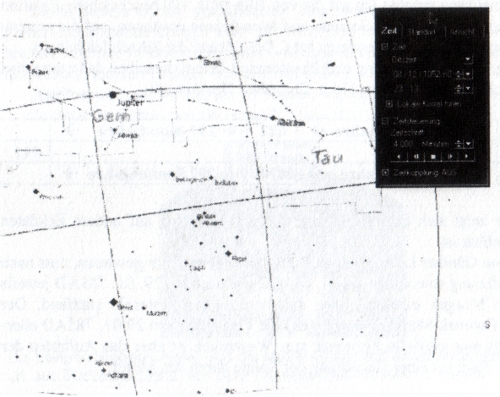
Drei Ereignisse in der obigen Liste habe ich mit zwei Planetariumsprogrammen nachgestellt und anhand der Angaben von Meeus zum Ereignis von 755 einen Eindruck zur Genauigkeit gewonnen.
Die Programme sind nicht geeignet, die Berechnungen von Meeus (d.h. die Jupiterverfinsterung) exakt nachzustellen. Die Programme sind aber mehr als ausreichend, die Stellung von Mond und Jupiter in der jeweiligen Konstellation darzustellen. Die folgenden Bilder habe ich mit RedShift 4™ erstellt. Der Einfachheit halber und in Unkenntnis tatsächlicher Beobachtungsorte (Durham? Jarrow? Chiaves?) habe ich Durham (1,6W/54,8N) in England als fiktiven Beobachtungsort angenommen.
Wie zu sehen ist, steht der durch den Mond bedeckte Jupiter für die Jahre 458 AD und 755 AD auf dem Stier, 1052 AD am Ende des Stieres in den heutigen Grenzen des Sternbildes Zwillinge! Dies ist eine den Jupiterkult repräsentierende Konstellation! Was ich meine, zeigen Plastiken des Jupiter Dolichenus [z.B. dolichenus]. Kenner des Kultes und seiner Varianten können weiterführende Überlegungen anstellen.
Ereignisdaten mit und ohne Phantomzeit
Bei Anwendung der Phantomzeit (PhZ) von Illig mit den Rändern 614 AD und 911 AD ergibt sich für die Daten der Ereignisse:
| Julianische Tageszahl JD |
Ereignis in A.D. – (Jul.) ohne PhZ |
Ereignis in A.D.- (Jul.) mit PhZ |
Sonnenjahre ohne PhZ |
Mondjahre zu 354 d |
| 1888652.5 | 07. 11. 458 | 20. 10. 158 | ||
| 1997148.3 | 23. 11. 755 | 07. 11. 458 | 300 Jahre | 309.5 |
| 2105643.4 | 08. 12. 1052 | 08. 12. 1052 | 594 (2 x 297) | 613 (2 x 306) |
| 2239269.4 | 14. 12. 1418 | 14. 10. 1418 | 366 | 378 |
Hypothetische tagesgenaue Eckdaten der PhZ, d.h. z.B. ein Übergang vom 31.08. 614 auf den 01.09. 911 sind hier nicht berücksichtigt, d.h. keine Betrachtung von Kalenderverwerfungen oder Kalenderkontinuität. In diesem Zusammenhang möchte ich auf die von Illig [2010, 450] beschriebene Relation zwischen den Skalen mit Sonnen- und Mondjahren erwähnen, auf die er mich dankenswerterweise hingewiesen hat („Die Lösung der Rätselgleichung“):
Illig: Hischra-Datierung und Phantomzeit liefern dieselben Jahresangaben wie ein Bezug auf das Jahr 325 n. Chr. ohne Phantomzeit:
| ← 297 Sonnenjahre → |
622 | ← 297 Mondjahre → | ||
| 325 | 911 | |||
| ← 297 Mondjahre → | 614 | ← 297 Sonnenjahre → |
Hier zeigt sich eine Beziehung, die nicht beliebig auf andere Eckdaten verschiebbar ist.
Schon Günther Lelarge hat im Web [lelarge] darauf hin gewiesen, dass nach Rückrechnung sowohl am 14. 01. 484 AD wie auch am 29. 01. 781 AD jeweils für den Morgen eine in Athen sichtbare Sonnenfinsternis stattfand. Der NASA-Espenak-Meeus-Katalog weist die Finsternis vom 29.01. 781 AD allerdings als eine partielle Finsternis aus. Wesentlich ist aber das Auftreten der 108495 Tage bei einer Bedeckung der Sonne durch den Mond.
Bei den oben betrachteten Jupiterbedeckungen durch den Mond dient Jupiter als langperiodischer Selektor und hat keinen eigentlichen Einfluss auf das Auftreten der Abstände von 108495 Tagen. Die Periodizität liegt in den Mondzyklen und in den Sichtbarkeitsbedingungen des Mondschattens auf der Erdoberfläche.
Eine Berechnung der zeitlichen Abstände der in einer Erdregion (Europa, Mittelmeer bis Mittelasien) rückgerechnet sichtbaren totalen und ringförmigen Sonnenfinsternisse der Jahre zwischen 181 AD und 1560 AD anhand einer visuellen Auswahl von Finsternissen nach Abbildungen aus dem Espenak-Meeus-Katalog habe ich gerade durchgeführt.
Die bisherigen Ergebnisse zeigen das überraschend häufige Auftreten der phänomenologischen Periode von 297a 15d. Wie sich zeigte, gibt es aber auch einen weiteren sehr gut passenden Maßstab mit einer Länge knapp unter 240 Jahren.
Schlussbetrachtung
Das mehrfache Auftreten von Zeitabständen von 297 Jahren und 15 Tagen der Termine von Doppelverfinsterungen von Mond und Jupiter ist bemerkenswert, gerade im Hinblick auf die von Illig postulierte Dauer der Phantomzeit. Denn die Zeitspanne erscheint hier als Ergebnis astronomischer Beobachtungen, die in früheren Zeiten gemacht worden sind, die heute berechnet werden können und nicht einmal selten sind.
Die in diesem Bericht geschilderten, lange verwehten Ereignisse und die großen Zeitabstände bringen eine im Abendland und Morgenland weit verbreitete Legende in Erinnerung [wiki / Siebenschläfer]. Ein Satz aus dem Koran nebst einem kleinen Bild der Betroffenen:

Die heiligen Siebenschläfer und die Mutter Gottes auf einem Votivbild des 19. Jh. aus Süddeutschland, aus dem Clemens-Sels-Museum in Neuss
„Dann erweckten wir sie, um zu wissen, welche der Scharen richtiger den Zeitraum berechne, den sie verweilt.“ [Sura 18:11]
Die Verweilzeit – der Zeitensprung der sieben Schläfer – hat, so glaube ich, mit der Dauerfrage der Zeitenspringer zu tun [in der Zeitschrift erstmals Topper 1994]. Im Koran wird vom 300 Jahre (309 Mondjahre) dauernden Schlaf der sieben Schläfer berichtet. Glauben bedeutet nicht Wissen, kann aber, im Idealfall, den Weg dahin ebnen.
Literatur
Ashbrook, J. (1972): About some early eclipse observations; Sky and Telescope, August 1972, p. 85
Demandt A. (1970): Verformungstendenzen in der Überlieferung antiker Sonnen- und Mondfinsternisse; Mainz
dolichenus = http://amstetten.at/Fotoalben/Jupiter%20Dolichenus/album/slides/28.Jup iter_Dolichenus.html
Espenak, F. / Meeus, J. (2009): Five Millennium Catalog of Solar Eclipses: -1999 to +3000, NASA Technical Publication TP-2009-214174
http://eclipse.gsfc.nasa.gov/SEpubs/5MKSE.html
Illig, H. (2010): Münzen zur Wikingerzeit. Drei Bezugsjahre für die Hidschra-Rechnung; Zeitensprünge 22 (2) 435-456
Krojer, F. (2003): Die Präzision der Präzession; München
lelarge = Lelarge, G. in https://groups.google.com/group/de.sci.geschichte/browse_th read/thread/8a2a520170cc9783/f0a73ff2d196d590?hl=de&q=millionenstadt+cord oba+group:de.sci.geschichte
Meeus, J. (1997): Mathematical Astronomy Morsels, Willmann-Bell Inc. Richmond, Virginia
Meeus, J. / Maanen, J. v. / Können, G.P. (1977): Occultations of planets by the eclipsed moon; Journal of the British Astronomical Association 87 (17) 135-145
MS139: http:/en.wikipedia.org/wiki/Historia_regum
Newton, R.R. (1972), Medieval Chronicles and the rotation of the earth, Baltimore
Topper, Uwe (1994): Die Siebenschläfer von Ephesos. Eine Legende und ihre Auswirkungen; Vorzeit-Frühzeit-Gegenwart 6 (1) 40-55






[…] Giesinger, Nobert: Mondfinsternisse und Jupiterbedeckungen. Ein Querverweis zur Phantomzeitdauer? […]